Quantum Numbers
Quantum numbers describe properties of a particle (eg. an electron) or a multi-electron system. They define the motion and trajectory of each electron, influencing characteristics such as ionization energy and atomic radius.
The wave function of an atom contains all quantum numbers of its electrons. According to the Pauli Exclusion Principle, no two electrons in an atom can have the same combination of for quantum numbers.
Unlike classical mechanics, where values can be continuous, quantum numbers only take on discrete values.
The Four Quantum Numbers
These four numbers fully describe hydrogen, the simplest atom:
- The Principal Quantum Number (n)
- The Angular Momentum Quantum Number (l)
- The Magnetic Quantum Number (ml)
- The Electron Spin Quantum Number (s)
Principal Quantum Number n
This number determines on which shell the electron is. In other words, the energy level and the most probable distance of the electron from the nucleus.
A larger n means:
- Higher energy
- Greater distance form the nucleus
- Larger atomic orbital
The principal quantum number must be a natural numbers: n=1,2,3,4…
It cannot be zero as an atom with no or a negative energy state cannot exist.
The value of n= 1 represents the K-shell in the Bohr model and is the lowest energy level.
Electron transitions
When an electron absorbs a photon, it jumps to a higher energy level (eg., from n=1 to n=2)
When an electron emits energy, it returns to a lower energy level (eg. from n=2 back to n=1)
Angular Momentum Quantum Number l
This number determines the shape of the orbital.
Think of an orbital as a room where electrons probably are. Click here to learn more about orbitals.
The angular momentum quantum number is always smaller than n and takes integer values : l=0,1,2,3…,(n-1)
You can also use letters instead of numbers to describe l.
- S: l=0
- P: l=1
- D: l=2
- F: l=3
Each value of l indicates a specific s, p, d, f subshell.
Principle shells and Subshells
The principle shell determines the level of the energy level of an electron and the distance from the nucleus. It is represented by the principle quantum number n.
The subshell is a division within the principle shell. The different subshells within the principal shell have specific shapes and can hold a certain number of electrons. It is represented by the angular momentum quantum number l.
Example
n=3 allows l= 0,1, 2, so it the third energy level has three subshells:
- 3s (l=0)
- 3p (l=1
- 3d (l=2)
Magnetic Quantum number ml
This number determines the spatial orientation of an orbital. It indicates the number of orbitals and their orientation within a subshell.
The value of ml can range from -l to l: ml= -l,…,0,…,l
For instance, if l=2, ml=-2,-1,0,1,ml
This means there are five orbitals in the d-subshell (l=2).
Electron Spin Quantum Number s
This number determines the instinct angular momentum (spin) of an electron.
The electron can either turn clockwise (s=1/2) or anti-clockwise (s=-1/2), thus s= ½ or -1/2
This is coherent with the Pauli Exclusion Principle.
Example for all quantum numbers
Helium has two electrons in the K shell.
The K-shell describes the lowest energy level and has the principle quantum number n=1
The electrons are in the s-orbital which is describes by l=0
This leads to ml=0
The electron spin quantum number needs to be opposite for the electrons (Pauli Exclusion Principle) , thus s=1/2 for the one electron and s=-1/2 for the other.
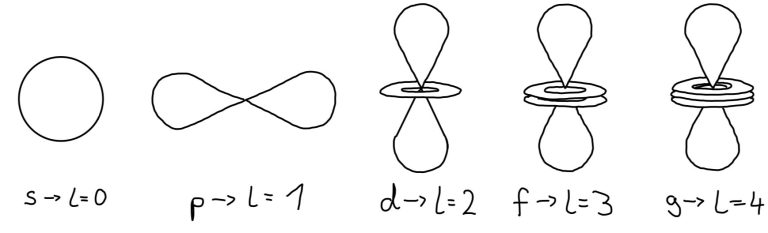



©Copyright. All rights reserved.
Wir benötigen Ihre Zustimmung zum Laden der Übersetzungen
Wir nutzen einen Drittanbieter-Service, um den Inhalt der Website zu übersetzen, der möglicherweise Daten über Ihre Aktivitäten sammelt. Bitte überprüfen Sie die Details in der Datenschutzerklärung und akzeptieren Sie den Dienst, um die Übersetzungen zu sehen.